こんにちは!Temaです(Twitter : @falmase)
今回はデッキ構築と確率についての記事です。「確率をデッキ構築に使ってみたい!」という方の助けになればと思います。
デュエルリンクスのプレイヤーなので特殊なルールの遊戯王で得た経験を元に話を進めますが、他のカードゲームに応用可能な考え方を中心に紹介します。
前回のヴェンデットの記事で登場した確率表も紹介します。確率表は私のオリジナル作品ですので、ブログ等へ画像を載せる方はこの記事を引用して頂けると嬉しいです!
↓↓前回の記事↓↓
ヴェンデット徹底研究
初手率早見表その1
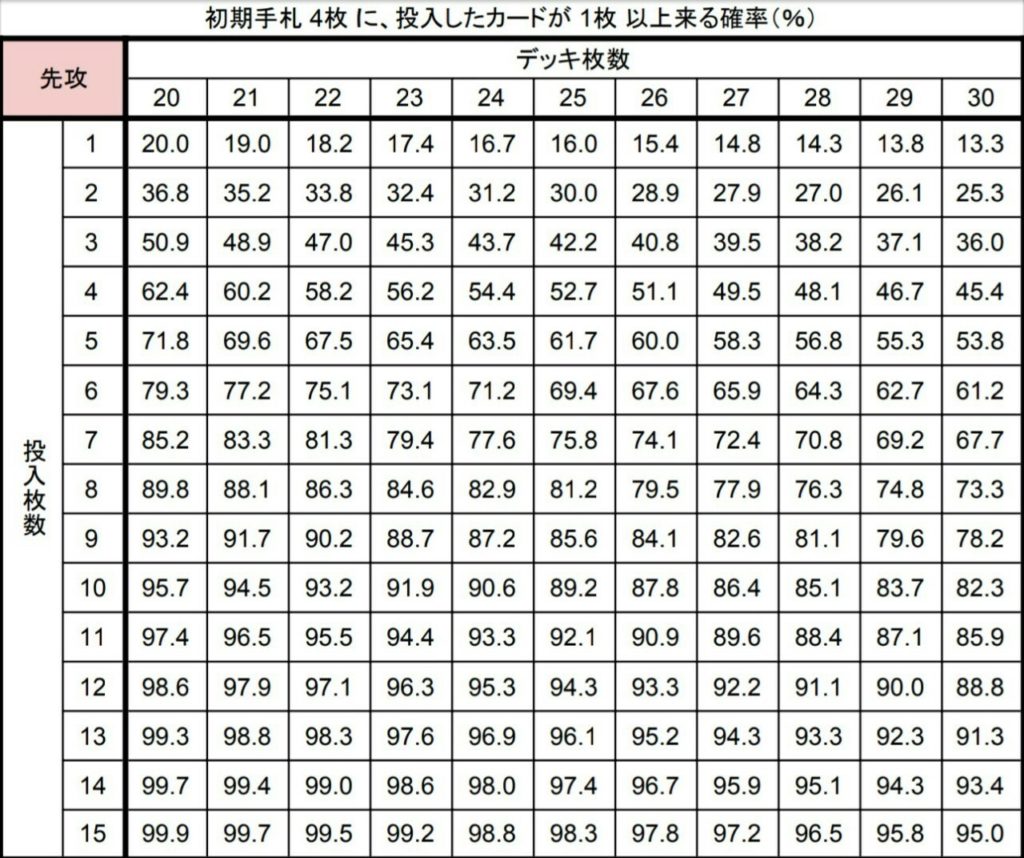
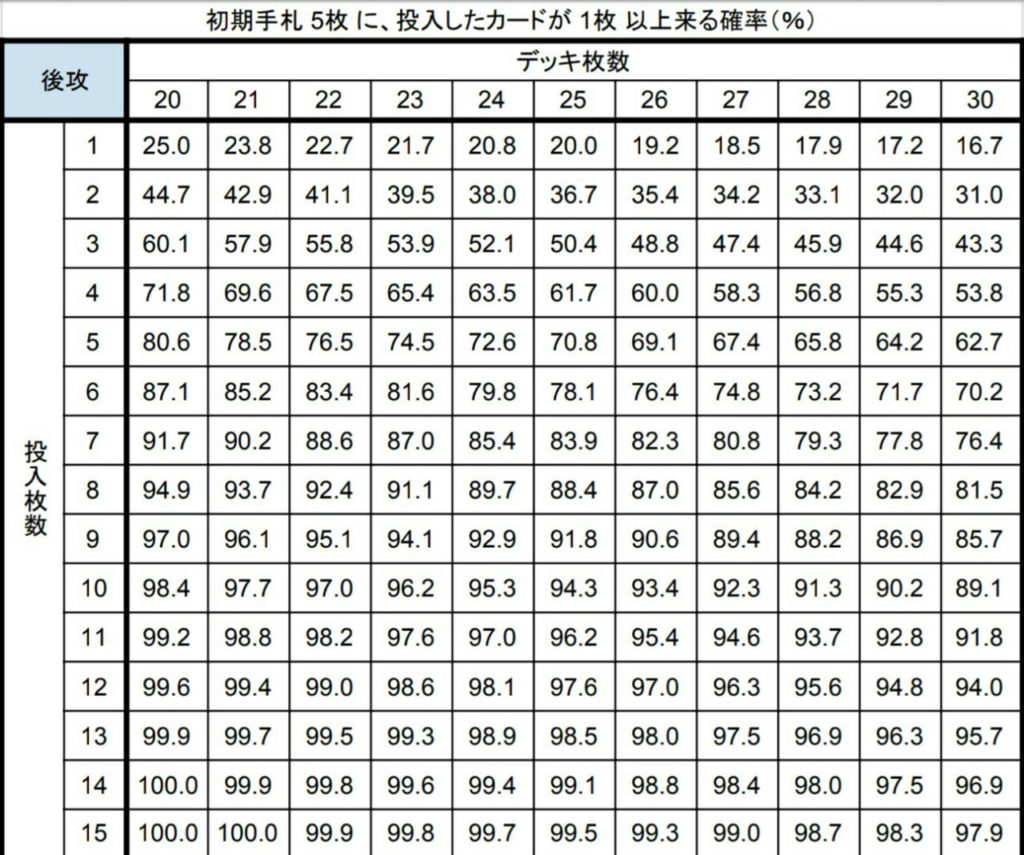
初手率早見表その2
デュエルリンクスのプレイヤーの方なら「さくっきーbot」をご存知かもしれません。闇団所属のトライスさんが開発したLINE専用botで、確率表を呼び出す機能があります。他にも様々な機能があるので、興味のある方は是非ご利用ください!
↓↓さくっきーbot取得はこちらから↓↓
さくっきーbot
この記事は次の構成で進めます。
❶ デッキ構築へ確率を活用する
❷ 確率表の紹介
まとめ
おまけ
❸ 計算式の解説
❹ 確率計算に意味はあるのか?
それでは本題へ移ります(/・ω・)/
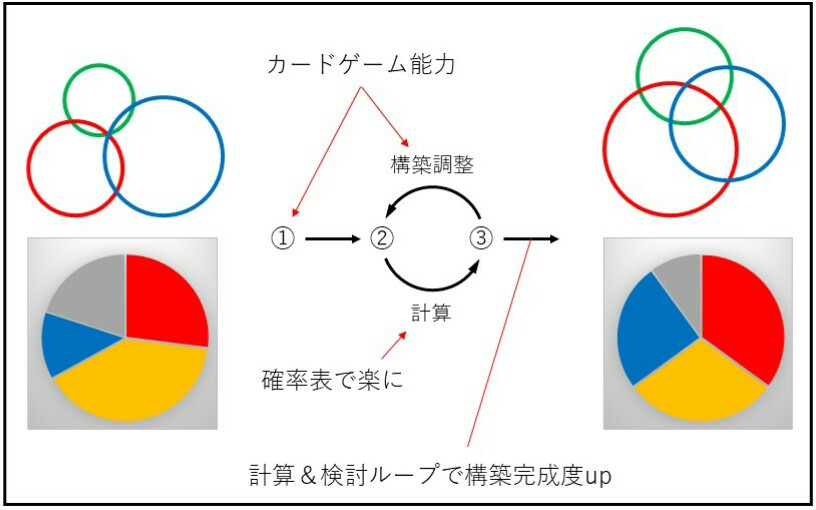
❶ デッキ構築へ確率を活用する
次の3ステップで活用します。
①ㅤ何の確率を知りたいか考える
②ㅤ確率計算を実行する
③ㅤ計算結果を解釈する
誰でも簡単にこの流れを実践出来るか?というと、そうではありません。
✲ 採用価値のあるカードを見つける能力
✲ 採用カードのテキストを理解する能力
✲ 複数カードの効果を組み合わせる応用力
✲ 作られる盤面の強弱を評価する能力
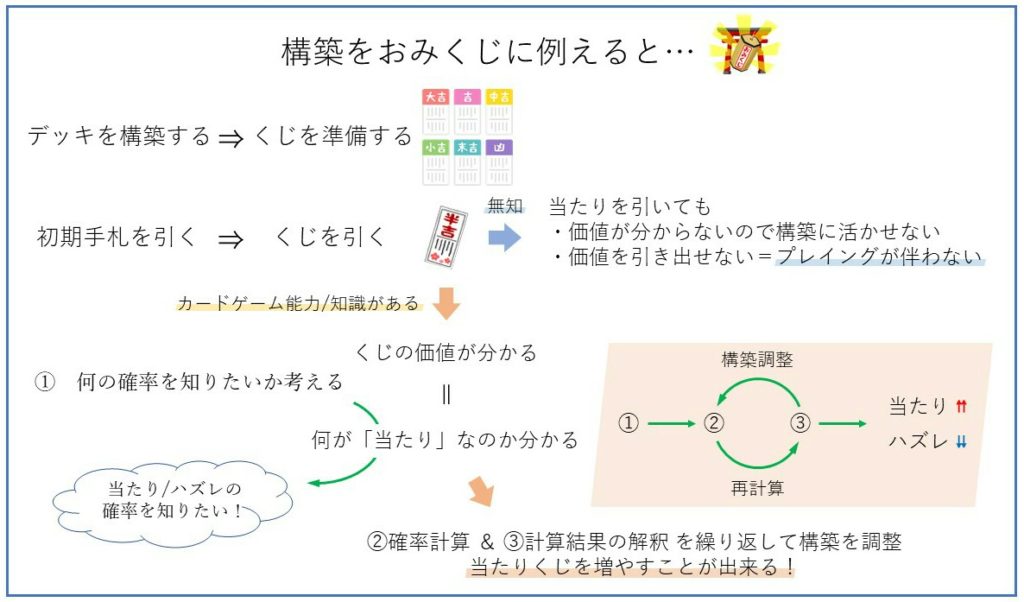
これらのカードゲーム能力や知識が必要です。構築をおみくじに例えた説明画像を作ったのでご覧ください。
「デッキを構築する」は「おみくじ箱の中にくじを準備する」と捉えることが出来ます。構築を調整するとおみくじ箱の中身が変化します。
「初期手札を引く」は「くじを引く」に対応します。
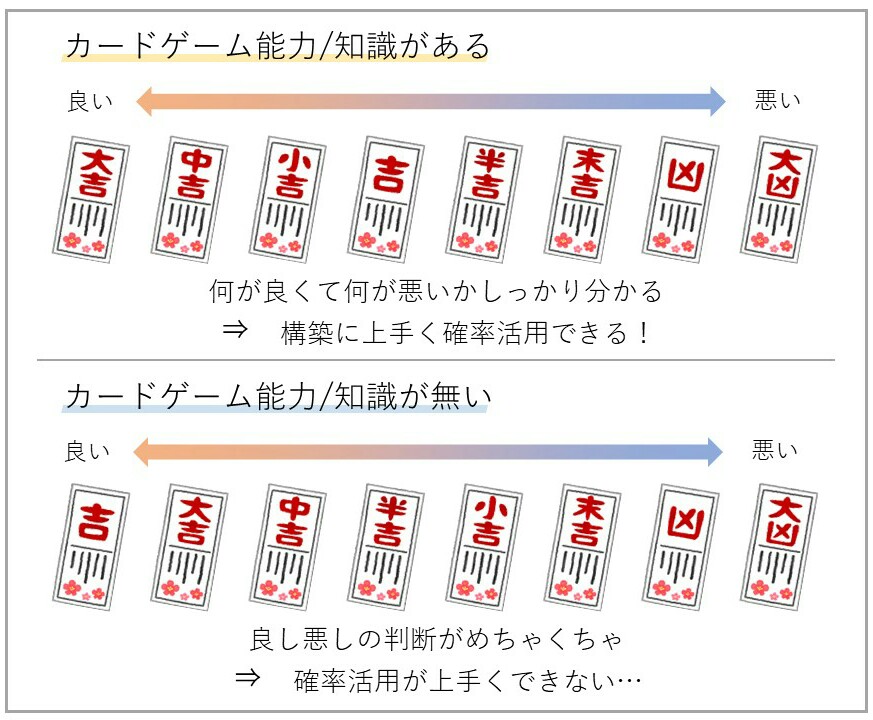
くじを引いても、くじを解読する能力や知識が無ければくじの良し悪しを判定することができません。くじの価値、つまり引いた初期手札の価値を理解するためにはカードゲーム能力や知識が必要です。
当たりくじを判別出来れば(①)、そのくじを引く確率を計算し(②)、結果を踏まえておみくじ箱の中身をどう変化させるか検討出来ます(③)。
カードゲーム能力や知識が無いと、確率を活用する①~③の流れに乗ることさえ出来ません。
まずはカードゲーム能力や知識を身に付けることを優先し、構築完成度を高める補助手段として確率を利用するというスタンスが大切です。
以下では①と③について少し掘り下げて話しを進めます。②については、計算を楽にする確率表を❷、よく使う数式をおまけ❸で紹介します。
①ㅤ何の確率を知りたいか考える
おみくじの例で言うと、「何が当たりか」を考えるステップです。いきなり自分で考えましょうと言われても難しいと思うので、具体例を紹介します。
◆ ◆ ◆
初期手札に
・モンスターが来る
・特定のカードが1枚以上来る
・防御札や妨害札が来る
◇ ◇ ◇
比較的分かりやすい「当たり」だと思います。構築の初期段階ではこの辺りの確率を見ると良さそうです。「モンスターが引けない!」とか「モンスターばかり来て防御札が来ない!」等の問題があれば、原因が数字で分かります。
デッキのコンセプトや強みについての理解が深まると、次のような確率も知りたくなるかと思います。
◆ ◆ ◆
初期手札に
・初動札が来る
・XとYがセットで来る
初期手札から
・理想的な動きが出来る
・最低限の動きが出来る
・幅広い動きを選択出来る
◇ ◇ ◇
これらが当たりであること、あるいはどれくらいの価値を持つ当たりなのかを判定するのは少し難易度が高いですが、ここでの判定精度が良いほど適切な確率活用が可能になります。
当たりの価値が分からないと構築を良く出来ません。
判定精度を良くするためにはやはり、カードゲーム能力や知識を身に付けることが大切ですね。
③ㅤ計算結果を解釈する
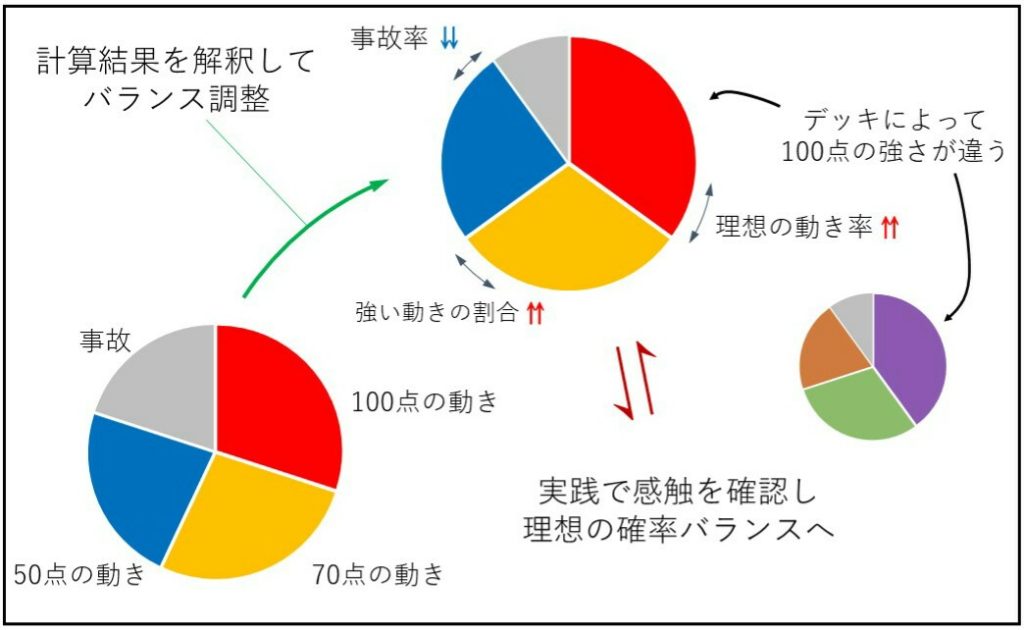
どうにか計算が完了したら、得られた計算結果を自分なりに解釈する必要があります。注意が必要なのは、当たりを判定する①の段階で当たりの可能性が無数に生まれていることです。「ある当たりXの確率がY%の構築が正解!」という答えは無く、自分で理想的な確率値を目指すのが基本です。
では、どうやって理想の確率値を目指せば良いのか?
一つの切り口として、おみくじに大吉・中吉・凶などがあるように、①で考えた「当たり」の価値に違いがあることを意識すると良いかもしれません。
◆ 例 ◆
理想的な動きが可能な初期手札を100点
最低限の動きが可能な初期手札を80点
事故や、ほとんど動けない初期手札を10点
「初期手札にこんな感じで価値の違いがあるかも?それぞれ確率計算すると…」
計算結果
20%で100点
65%で80点
15%で10点
「理想の動きが20%だと環境トップシェアのデッキに負け越しそう。採用枚数を考え直すか…」⇒ 再試行
◇ ◇ ◇
このように場合分け&大体の点数付けをすると、デッキ全体の確率バランスを意識しながら各初期手札の確率値を解釈することが可能になり、理想的な確率を探求する手掛かりになるかもしれません。
デッキ全体の確率バランスについても正解は無いですが、自分好みのタイプはあると思うので、そこを目指して調整すると回し心地が良くなるかもしれません。
構築A
60%の確率で100点
30%の確率で50点
10%の確率で10点
⇒ 理想ムーブを積極的に狙うタイプ
構築B
40%の確率で100点
45%の確率で80点
15%の確率で10点
⇒ 準理想形も用意するタイプ
環境で活躍するデッキは上の二つのようなタイプが多い気がします。バリバリに尖らせたAのタイプよりも、手広く展開を選べるBのタイプが個人的には好きです。
構築C
50%の確率で100点
50%の確率で80点
⇒ 安定を目指すタイプ
Cのタイプは一見強そうですが、あるデッキの理想の動きを100点と設定する場合は別のデッキの100点と強さが違います。このタイプは他のデッキよりも100点が弱くなければ作れないことが多いです。
Cのタイプに限らず、どのタイプでも環境で通用する100点なのかを見極めるのが大事ですね。
また別の切り口として、理想的な事故率をベースに考えながら初期手札の確率バランスを整えるのも良いかもしれません。事故率がある程度低いことも良いデッキに共通している要素です。
事故率は特に連勝を必要とする場合に意識する必要がある要素です。例えば5連戦する場合、事故率20%と10%では以下のような差があります。
◆ ◆ ◆
・事故率20%で5回連続事故しない確率
80% × 80% × 80% × 80% × 80% ≒ 33%
・事故率10%で5回連続事故しない確率
90% × 90% × 90% × 90% × 90% ≒ 59%
◇ ◇ ◇
事故しない時に必ず勝てる訳では無いので、連勝を狙うなら「連続非事故率が高く、事故でない時の動きが十分に強いデッキ」を作る必要があります。
理想的な事故率を10%と設定すると、調整中のデッキの事故率が高いか低いかを解釈する基準が出来ます。先ずは事故率10%以下を目指し、残りの90%の配分を後で検討するという流れで構築調整を進める方針も良いかもしれません。事故の定義は人それぞれ、デッキそれぞれなので、何を事故と判定するかも大事ですね。
少し脱線になりますが、事故率を下げることに執着して中~終盤に必要なカードを削り過ぎるのは良くないです。初期手札に来ると弱いけれど、中~終盤デッキに残っていればサーチ選択幅が広がり、状況次第で強力に機能するカードもあります。このようなカードを単に削るのではなく、採用枚数を減らしながらデッキ総枚数を増やす等の工夫で初期手札率を調整し、採用継続を試みるのも一つの手だと思います。
初期手札で作られる盤面だけでなく、数ターン先を見据えた構築の方が良い勝率を出す場合もあるので、目先の安定に惑わされないように気を付けましょう。
以上のように確率計算の結果を自分なりに解釈し、「各カードの採用価値/理由/枚数の再検討&構築調整 ⇒ 再計算」を繰り返すことでデッキ完成度を高めて行くのが確率活用の理想だと思います。
自分にとって理想的な確率バランスを持つデッキを目指すためには、実践で感触を確かめるのも大切です。好感触を得られると確率に対する納得度が高まり、どの程度の確率なら自分が満足出来るかも掴めてくるので、適度に実践も取り入れましょう。
❷ 確率表の紹介
ここまでの話をよく読んだ方もそうでない方も
確率計算、めちゃ面倒では?
と感じているのではないでしょうか。
まじで面倒くさいです。
私は楽をしたい人間なので、計算の過程を極力減らそうと思いました。幸いなことに表計算ソフトの嗜みがあったので、それを利用して早見表が作れないかと閃きました。

↓↓画像とスプシ取得可能です↓↓
初手率早見表1と2、初手率早見表3~8
閃いてから10分でベースが完成…なぜもっと早く作らなかったのか…
なにがともあれ、確率表を活用することで計算過程を大幅に短縮可能に!すごい!楽ちん!
画像は遊戯王デュエルリンクス用となっていますが、エクセルファイルの計算式をいじれば他のカードゲームにも応用可能です。(詳しくは ❸で)
見るだけでわかる方も居ると思いますが、早見表の使い方を簡単に紹介します。基本的には上のデッキ枚数に対してあるカードを横の採用数で入れた場合、表の上部に書いてある条件を満たす確率が各マスに表示されています。
────────────────
① 1枚以上来る確率
初手率早見表その1

初手率早見表その2

私はこれを一番よく使います。あるカードを x 枚デッキに入れた場合に初期手札に入る確率を調べられます。「防御札」「初動札」「序盤で引きたくないカード」など特定の役割を持つカードを沢山デッキに入れることもあるので、投入枚数を15まで表示しています。
────────────────
② 1枚だけ来る確率
初手率早見表その3
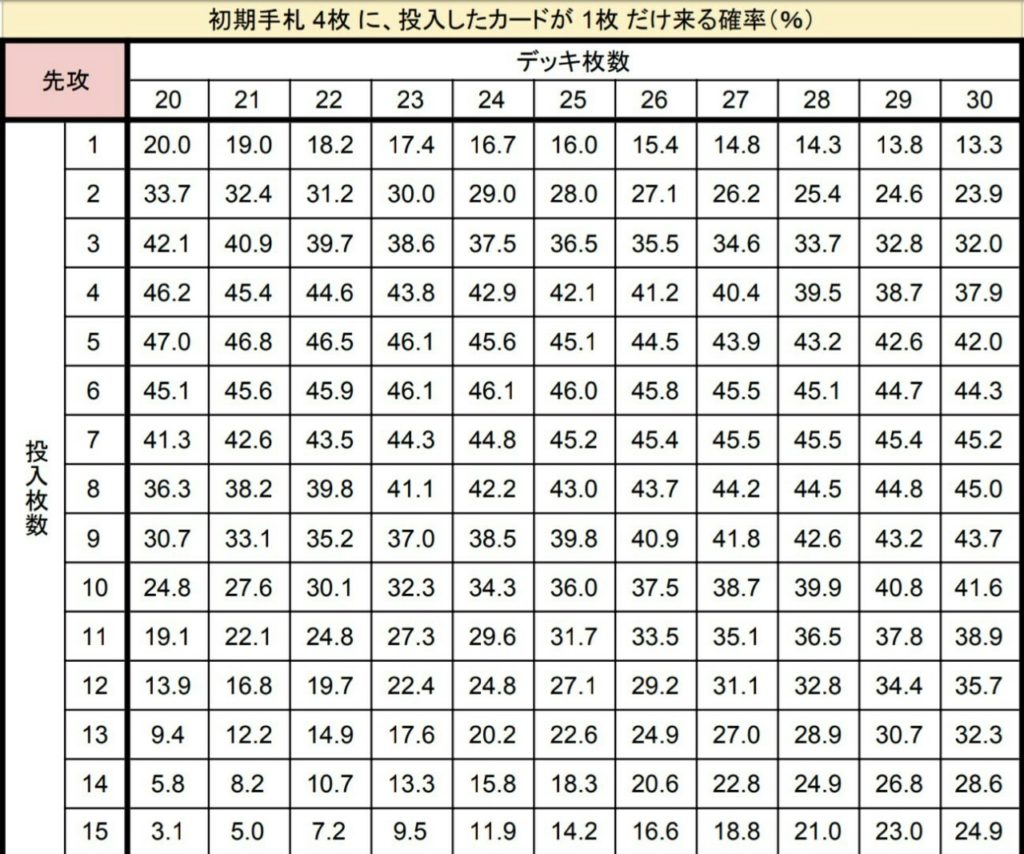
初手率早見表その4
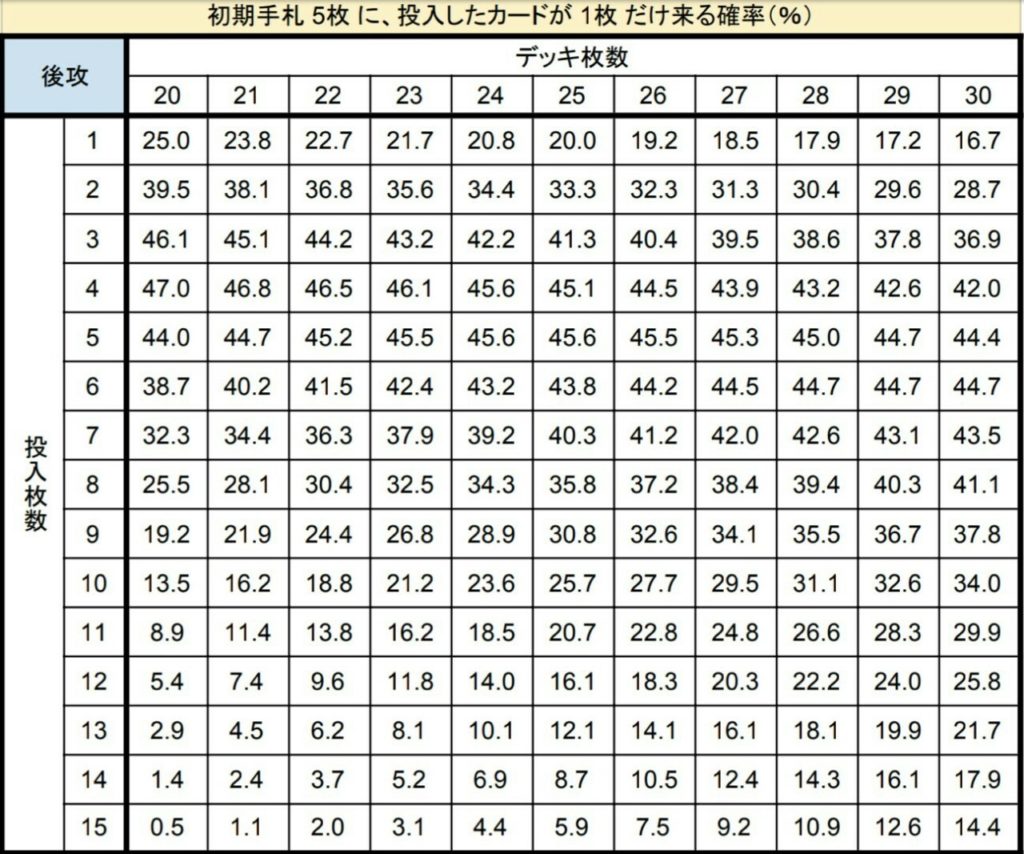
序盤に2枚以上引きたくないカードがある時はこちらも確認します。
────────────────
③ 2枚以上来る確率
初手率早見表その5
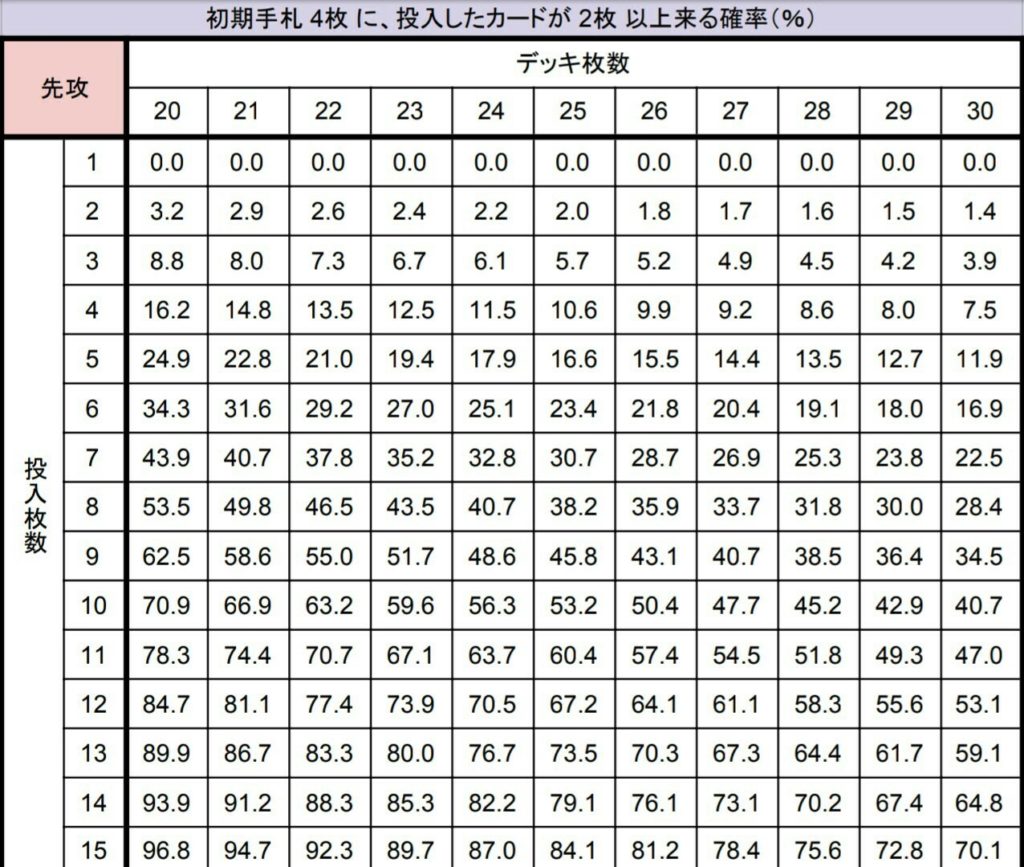
初手率早見表その6
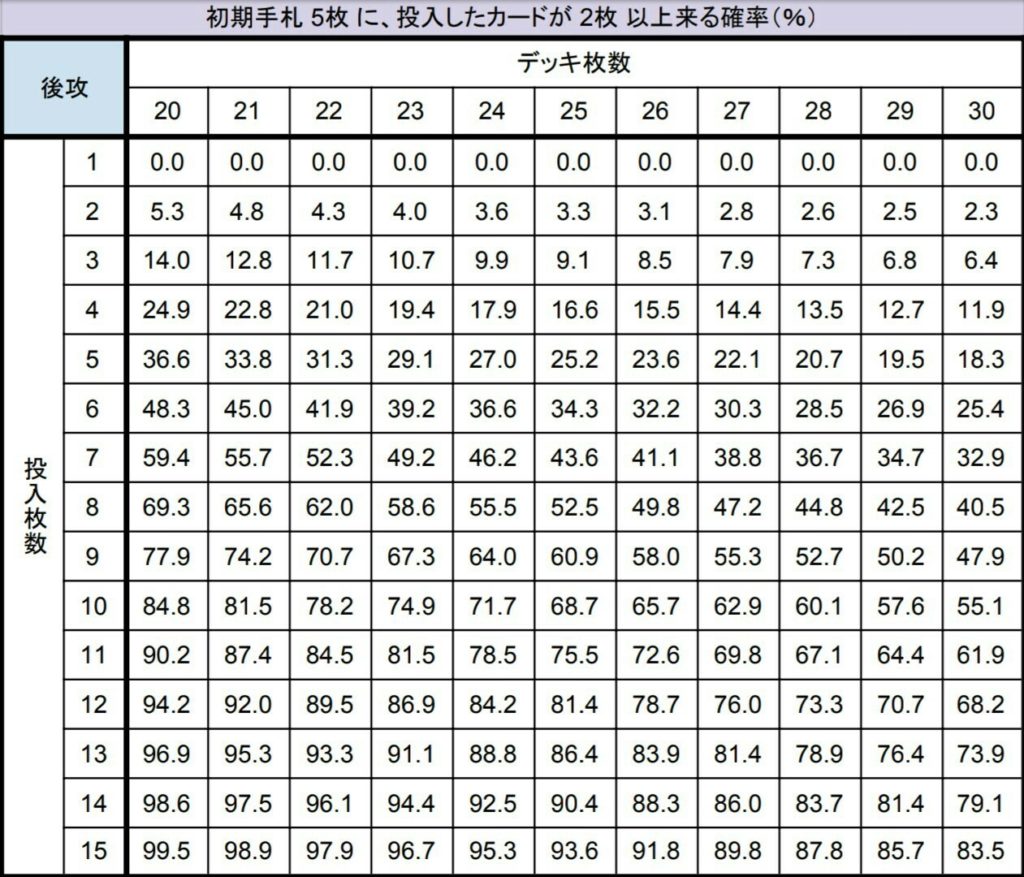
2枚以上引きたいカードを考えるときに見ます。
────────────────
④ 2枚セットが来る確率
初手率早見表その7
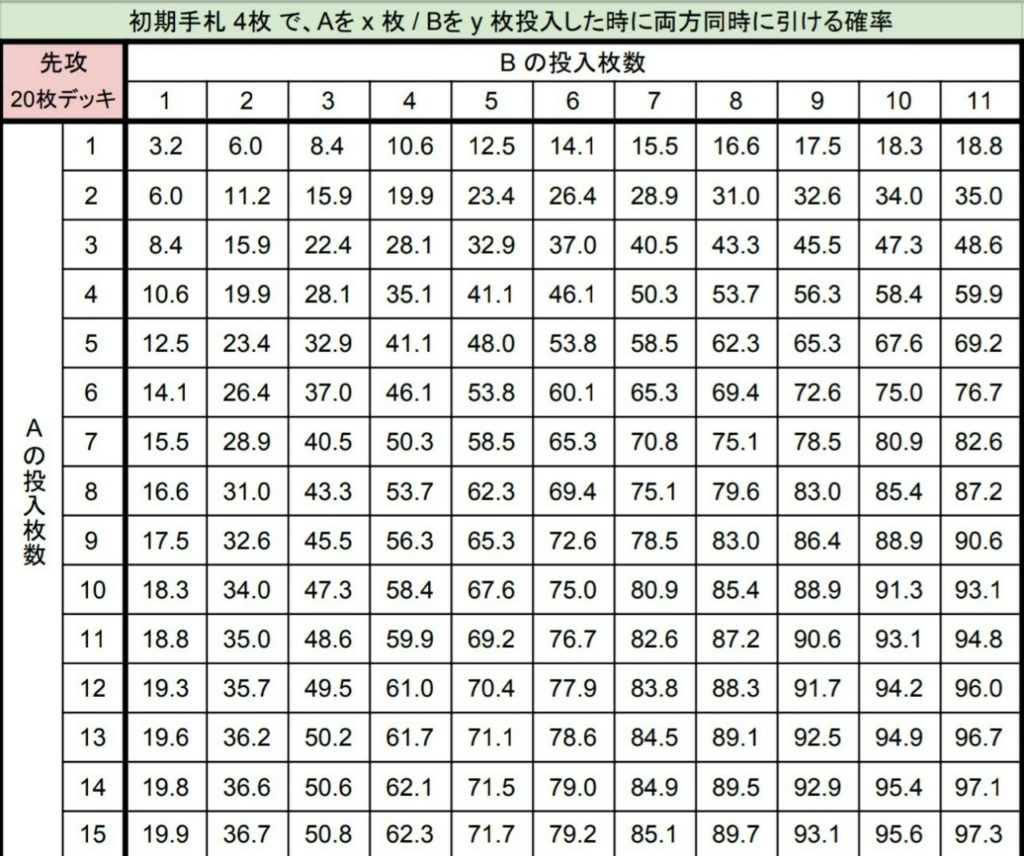
初手率早見表その8
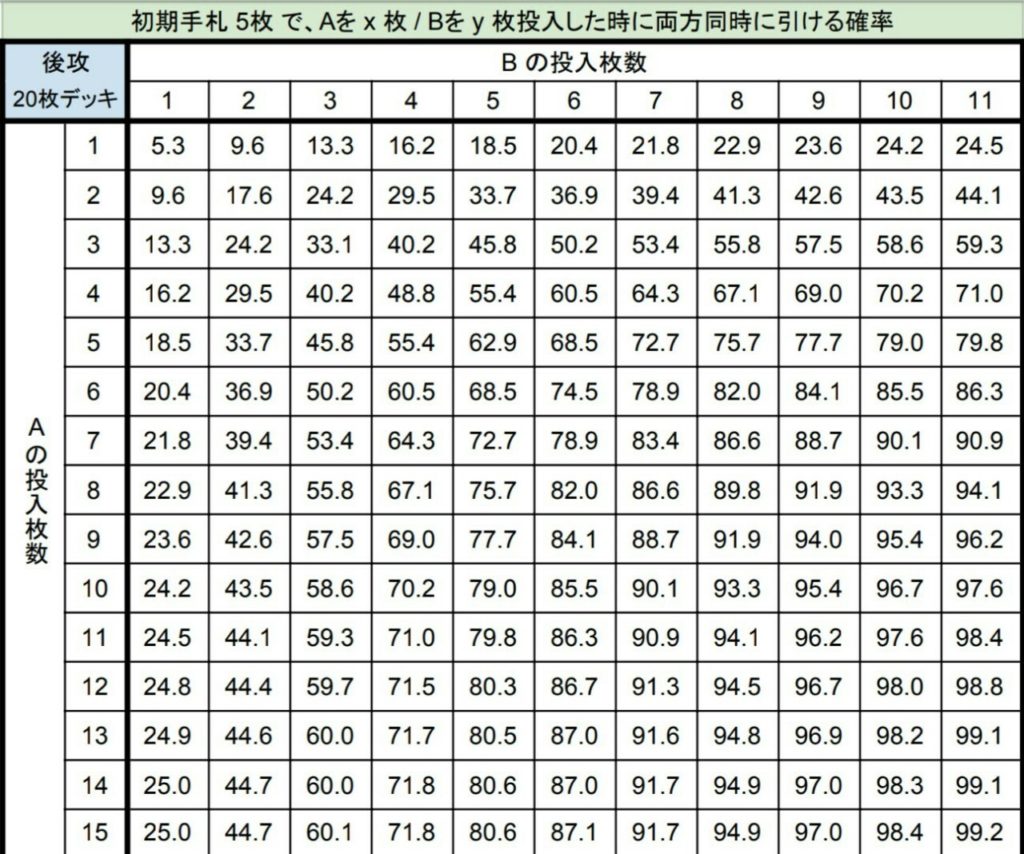
2枚セットで来ると強い動きが出来るようなカードを何枚ずつ採用するかを見たい時に便利です。上の画像は20枚デッキ用の表示ですが、エクセルファイルのパラメーターを変更することで別のデッキ枚数の表も作成可能です。OCGや他のカードゲームでも役立つかも。
パラメーター表
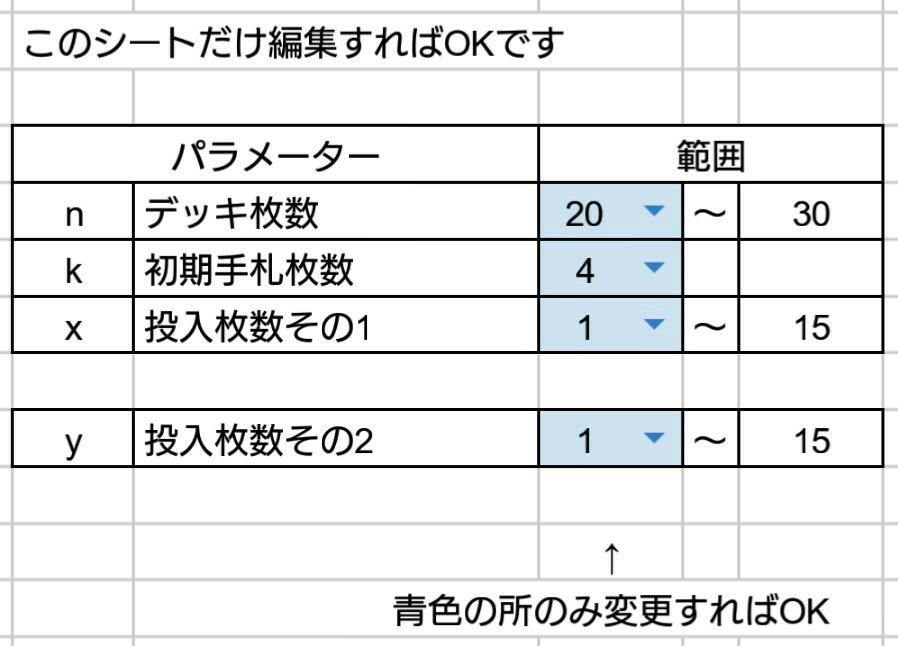
*以下エクセルファイルとなります。
*カードゲーム用確率計算シート(クリックしてダウンロード)
────────────────
それぞれ先攻・後攻両方の確率表を作っていて、両方利用することでより実践的な確率を求められます。
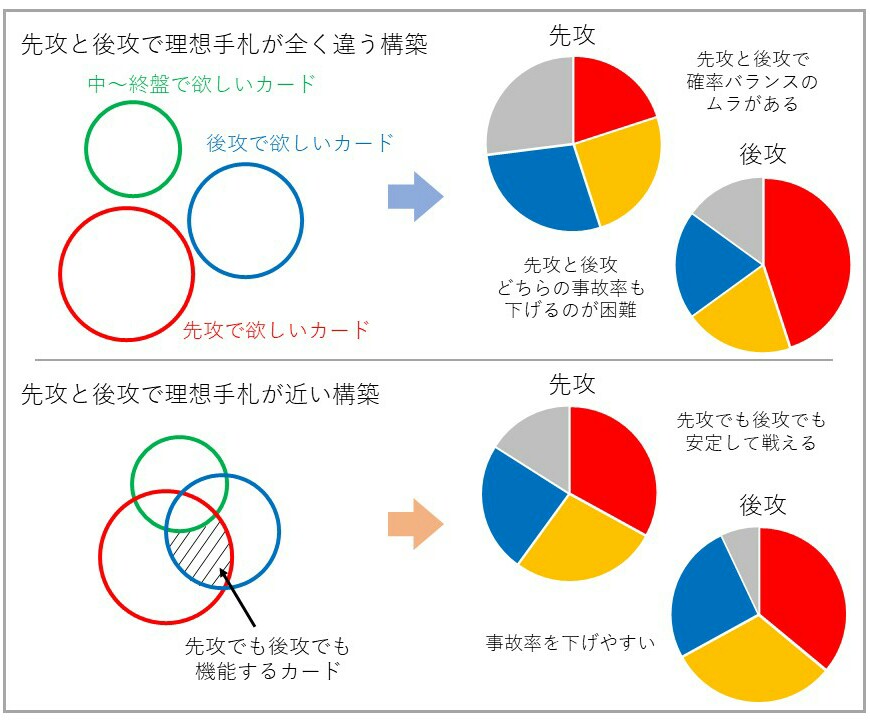
余談になりますが、先攻と後攻で要求手札の差が大きいと構築が大変です。先攻理想形と後攻理想形の実現率に乖離が生じ、どちらも高めることが困難になります。前回の記事で紹介させて頂いたヴェンデットが環境で戦えたのは、先攻・後攻両方の理想手札にあまり差がなかったという部分も大きかったです。
カードごとに「先攻で役割を果たすもの」「後攻で役割を果たすもの」「両方で機能出するもの」があるので、構築の際に意識してみると良いかもしれません。
基本的に先攻理想形が弱いデッキやテーマは勝率面で安定を得られず、環境から淘汰されます。逆に先攻理想形がしっかりしたデッキは(少なくとも今のリンクス環境であれば)後攻でも同様の動きを目指すことで十分に戦える場合が多いです。
まとめ
・3ステップで確率活用
・カードゲーム能力や知識が必要
・計算&検討ループで構築完成度up
・計算は確率表で楽に出来る
本記事のメインの話は以上となります。読んで頂きありがとうございました!
おまけ
❸ 計算式の解説
ここでは数学的な話をします。興味のない方は読み飛ばして大丈夫です。
計算式さえ理解できれば、デッキ枚数・投入枚数・初期手札枚数というパラメーターの変更により、他のカードゲームへの応用が可能です。以下のエクセルファイルには式を書き込んであるので、各パラメーターを変更するとそれに応じた結果が得られます。
↓↓カードゲーム用確率計算シート↓↓
*カードゲーム用確率計算シート(クリックしてダウンロード)
スプレッドシートが好みの方は下記のツイートから取得可能です。
↓↓ツイートから画像取得可能です↓↓
初手率早見表3~8
エラー回避のためいくつか余計な関数が入っていますが、本質的にやっていることは以下で記述する内容と同じです。
それでは懐かしい数学の時間です…
パラメーターは次のアルファベットと対応しているものとしてご覧ください。
n = デッキ枚数
x = Xの投入枚数
y = Yの投入枚数
k = 初期手札枚数
計算で活躍するのは次の関数です。
nCk : n 個から k 個を選ぶ組み合わせを計算
例 20C4 = 20 × 19 × 18 × 17 ÷ 4 ÷ 3 ÷ 2 ÷ 1
詳しくは下記のサイトに分かりやすく説明されていますので、興味のある方はご覧になってください。
コンビネーション関数について
外部リンク
Xを引く確率の計算は基本的に面倒で、Xを引かない確率の計算は簡単です。引く確率の計算はXを何枚引くかで場合分けが必要ですが、引かない確率の計算ではXを除いたカードで作られる全組み合わせを上記の関数で計算するだけで済むためです。
以下では極力、引かない確率の計算を利用して行きます。
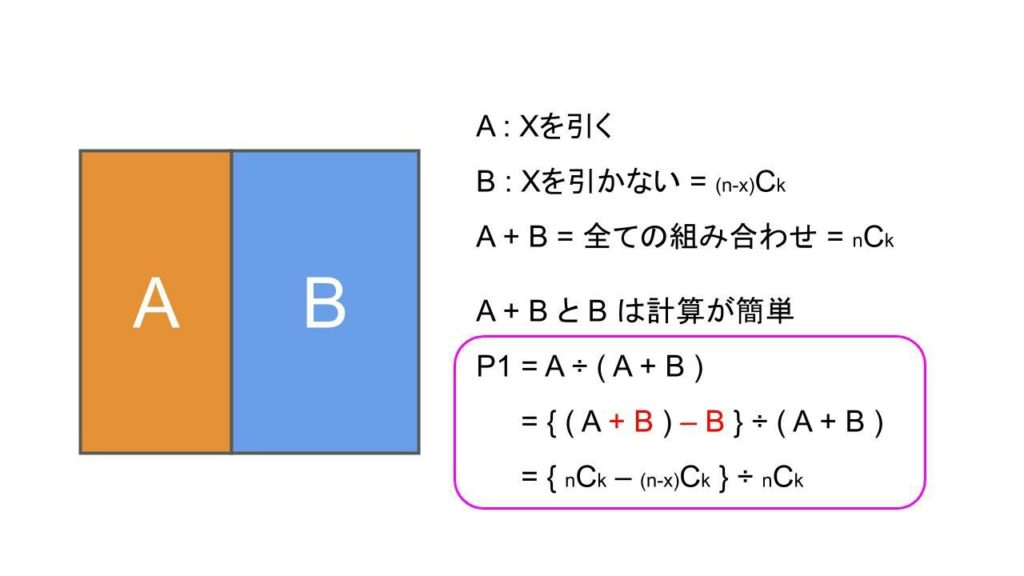
① Xが1枚以上来る確率 P1
{ nCk - (n−x)Ck } ÷ nCk = P1
式の説明
全ての初期手札の組み合わせ ( A + B ) から初期手札にXが無い組み合わせ ( B ) を引くことでXを引く組み合わせ ( A ) を計算しています。注意が必要なのは、Xを引く枚数については一切考えておらず、Xが1枚以上来る組み合わせを計算しています。得られたXを1枚以上引く組み合わせ ( A ) を、全ての初期手札の組み合わせ ( A + B ) で割ることで確率 ( P1 ) が得られます。
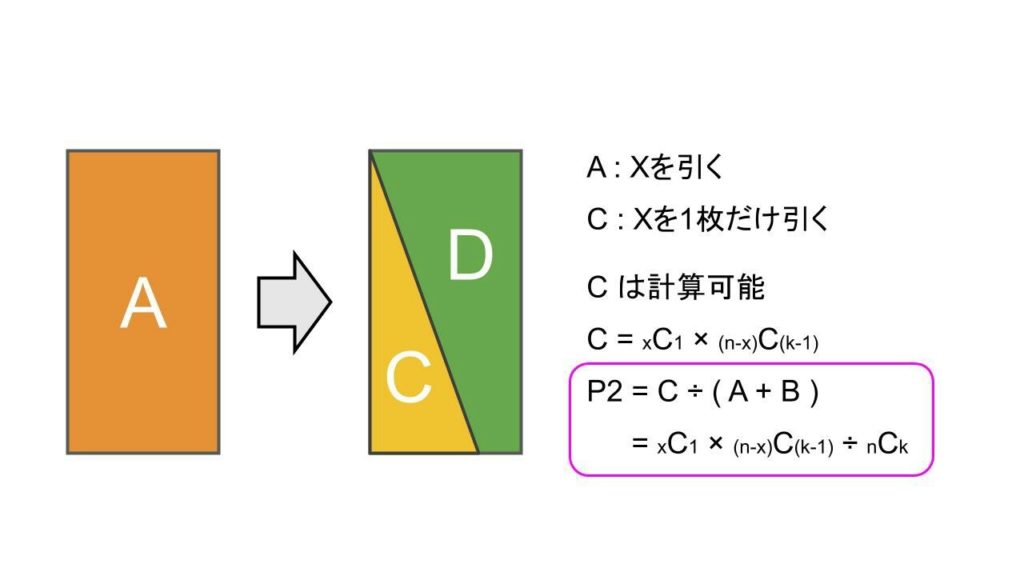
② Xが1枚だけ来る確率 P2
xC1 × (n−x)C(k−1) ÷ nCk = P2
式の説明
x 枚からどのXを選ぶかの組み合わせ ( xC1 ) と、残りの手札をX以外のカードで作る組み合わせ ( (n−x) C (k−1) ) を掛けることで、初期手札にXが1枚だけ来る組み合わせ ( C ) が得られます。これを全ての初期手札の組み合わせ ( A + B ) で割ることで確率 ( P2 ) が得られます。
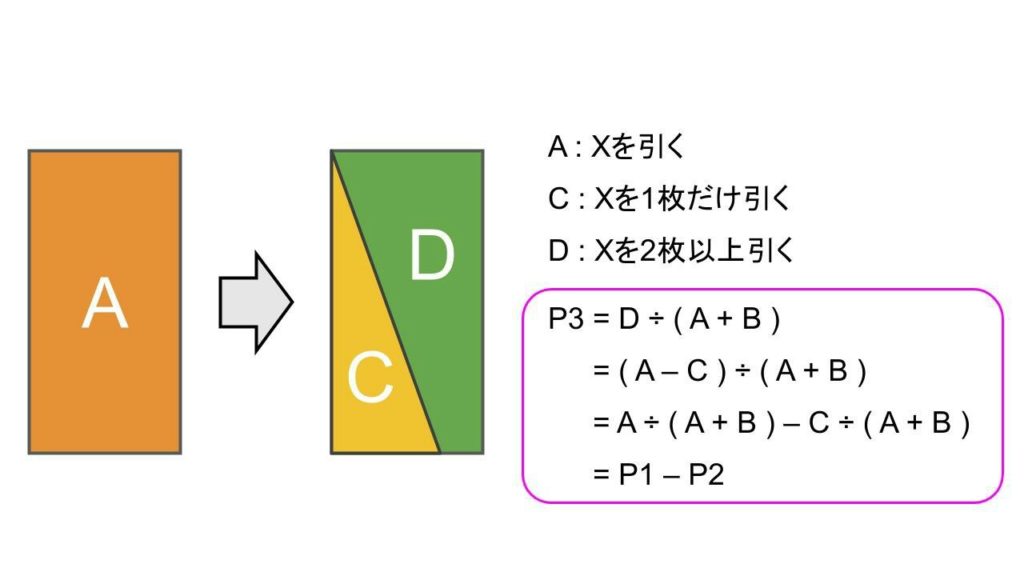
③ Xが2枚以上来る確率 P3
P1 − P2 = P3
式の説明
初期手札にXが1枚以上来る組み確率 ( P1 ) から1枚だけ来る確率 ( P2 ) を引くことで2枚以上来る確率 ( P3 ) が得られます。
④ XとYがセットで来る確率 P4
{ nCk - (n−y)Ck - (n−x)Ck + (n−x−y)Ck } ÷ nCk = P4

式の説明
初期手札にXとYがセットで来る組み合わせ ( E ) を直接計算するのは難しいです。一方で、XもYも引かない組み合わせ ( H ) は簡単に計算できます。Xのみを引く組み合わせ ( F ) は、Yを引かない組み合わせ ( F + H ) から ( H ) を引くことで計算可能です。Yのみを引く組み合わせ ( G )も同様に、 ( G + H ) から ( H ) を引くことで計算可能です。
全ての組み合わせ ( E + F + G + H ) に
( F ) = ( F + H ) - ( H )
( G ) = ( G + H ) - ( H )
を代入し、式を整理することで ( E ) が得られ、これを全ての初期手札の組み合わせ ( A + B ) で割ることで確率 ( P2 ) が得られます。
以上が❷で紹介した表で使われている計算式のベースになっています。毎回こんな計算していると死んでしまいますね。表計算ソフトを上手く利用するとこんな計算一切せずに表が仕上がるので感動です。
❹ 確率計算に意味はあるのか?
おまけパートその2です。「確率計算意味あるの?」とよく言われるので、独り言レベルですが私の意見をまとめて置いておきます。
一定の割合で「結局は運でしょ?カードゲームに確率計算の意味あるの?」と言う方が居ます。「結局は運」という部分は間違いありませんが、以下を例に少し考えます。
◆ くじ引き ◆
・箱A:100本中当たりが3本
・箱B:100本中当たりが5本
◇ ◇ ◇
箱Aに挑戦して当たりを引く人は3人
箱Bに挑戦して当たりを引く人は5人
確率計算に意味がないと感じる方は、箱Bに挑戦して外れた95人側の立場から箱Aに挑戦して当てた3人を見る気持ちの方が多いのではないでしょうか。
本当に箱Bに挑戦することに意味がないのか?
最終的に結果を決めるのは運であることに間違いありませんが、当たりを引く可能性を高めるためにどちらの箱がより良いかを選択する「確率計算に基づく意思決定」に意味がないと私は思いません。
別の見方をすると、箱Bに挑戦し続ける人は箱Aを引き続ける人よりも成功する回数が多くなります。
箱Aに100回挑戦して当たる回数は3回
箱Bに100回挑戦して当たる回数は5回
数回の上振れや下振れに惑わされず、長い目で見たときの成功回数に目を向けると確率計算の良さを感じられるかもしれません。
成功を引き続ける上振れも成功確率がより高い方に挑戦する方が狙えます。大会等で勝ち上がるには上振れ運も重要で、その運を呼び込む準備として確率計算をデッキ構築に取り入れるのは意味のある行為だと思います。
確率計算に意味がないと感じる方の中には、構築を調整することで別の価値を持った当たりが出現することを本能的に感じ取っている方も居ます。いちいち確率計算や価値評価をするくらいなら戦いながら感覚で調整すれば良いと考えるタイプですね。調整方法の好みの問題なので、お互いの調整方法に違いがあることを尊重するのが良いと思います。
また、「結局はプレイングでしょ?確率計算とかあんまり意味なくね?」と言う方もいらっしゃいます。確かに、入念に確率計算された素晴らしい構築でもプレイングが伴わなければ価値が発揮されませんが、私は勝利に必要な要素を以下のようにイメージしています。
構築 × プレイング × 相性 × 精神力 × 時の運 > 相手
プレイングと構築は独立した要素で、それぞれを高めることに別々の価値が生じると私は思います。強くなることを目指すなら他の成長させることが困難な要素ではなく、学習により成長可能な構築とプレイングの両方を追求し、総合力を高めるのが重要ではないでしょうか。
他には、確率にひどく裏切られた過去を持つ人も否定的なことをおっしゃる場合があります。時には確率に裏切られることもありますが「外れる可能性が少しでも有れば外れる」と割り切ることも大事です。確率計算したデッキを信じましょう。連続で事故っても不運な下振れだと理解できれば、デッキの構築を疑って迷走することが減り、精神的に少し楽になれます。これも確率計算で得られる恩恵の一つかなと思います。
本記事の内容は以上となります。お疲れ様です…
最後までお付き合い頂いた方、ありがとうございました!
あとがき
私が確率を抵抗なく扱えたのは高校の時に数学の授業を聞いていたおかげかと思います。何の役にも立たないだろうと感じる勉強でも、後から恩恵を感じられることがあると学びました。将来の自分への投資だと思って、少しだけ勉強を頑張るのも良いかもしれません…
最後まで辿り着く人が少ない記事ばかり量産しそうで将来に不安がありますが、次回以降はこの記事で言及していたカードゲーム能力や知識について、あるいは自分なりの構築論について書いてみようかなと思います。

コメント